Circle and Rotated Rectangle Collision Detection
Circle and Rotated Rectangle
I’m going to explain how to implement collision detection for circle and rotated rectangle. Collision detection is determining if object A is hitting object B. A circle has center x y position with a radius. A rectangle contains left top x y position, width, height, and the angle to be rotated with. We assume a rectangle rotates around its center point.
I will use applet, pictures, and code to show this. I read this article as a reference to understanding collision detection between a circle and a rectangle not rotated.
Sample Applet
Here is a sample Applet to demonstrate collision detection. If collision is detected, the shapes turn blue. The green outlined shapes represent the state used to calculate. The orange line connects the center of unrotated circle to the closest point on rectangle. You can type in an angle and press the button to rotate. Click and/or drag anywhere to move the circle.
Implementing collision detection with a circle and rectangle with angle
The idea is simple. To perform the calculation, We need to have both shapes at the position when rectangle has 0 degree. It gets a little complicated if we rotate the rectangle with an angle. It’s easier to keep the rectangle straight with 0 degree to locate other points with simple addition. Top left is (x, y), top right is (x + width, y), and bottom left is (x, y + height).

Instead of rotating rectangle, rotate the circle back with the angle we were going to rotate rectangle. Put the circle’s center point to where it would be when rectangle’s angle is 0. Single point is easy to rotate. Looking at the rough picture, Blue shapes represent when rectangle is rotated and actually what we will see. Black shapes are used for calculation. We adjust the shapes with 0 degree or in other words, leaving the rectangle with 0 degree and rotating the circle back with rectangle’s angle instead.
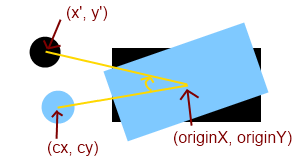
The formula I used is below. Variable cx/cy stand for circle’s center point, originX/originY are the point we rotate the circle around, and x’/y’ are the rotated point.
x’ = cos(theta) * (cx – originX) – sin(theta) * (cy – originY) + originX
y’ = sin(theta) * (cx – originX) + cos(theta) * (cy – originY) + originY
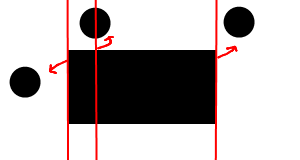
Find the closest point from the unrotated circle and the rectangle. All we need to do is if-else comparisons for x and y separately.
For x, we use rectangle’s left x (rx) and right x (rx + width) to compare with circle’s center x (cx). If cx is on the left of rx, then rx is the closest x. Otherwise if cx is on the right of rx + width, then closest x is at rx + width. Finally, if none of 2 cases match, closest x point is cx itself. In the picture below, the red line is where the x will lie on.
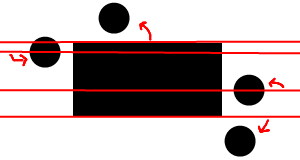
The same rule applies for y. If circle’s center y (cy) is above top y (ry), ry is the closest y point. If cy is below the bottom y (ry + height) point, ry + height is the closest y point. If these cases don’t match, the closest y point is cy itself.
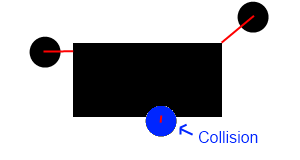
Lastly, we need to compute the distance from the unrotated circle’s center to the closest point we found earlier. I used the Pythagorean theorem to find that distance (a^2 + b^2 = c^2). Then you compare it with the circle’s radius. If distance is smaller than radius, the 2 shapes are colliding.
Sample Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 | // Rotate circle's center point back double unrotatedCircleX = Math.cos(rect.angle) * (circle.x - rect.centerX) - Math.sin(rect.angle) * (circle.y - rect.centerY) + rect.centerX; double unrotatedCircleY = Math.sin(rect.angle) * (circle.x - rect.centerX) + Math.cos(rect.angle) * (circle.y - rect.centerY) + rect.centerY; // Closest point in the rectangle to the center of circle rotated backwards(unrotated) double closestX, closestY; // Find the unrotated closest x point from center of unrotated circle if (unrotatedCircleX < rect.x) closestX = rect.x; else if (unrotatedCircleX > rect.x + rect.width) closestX = rect.x + rect.width; else closestX = unrotatedCircleX ; // Find the unrotated closest y point from center of unrotated circle if (unrotatedCircleY < rect.y) closestY = rect.y; else if (unrotatedCircleY > rect.y + rect.height) closestY = rect.y + rect.height; else closestY = unrotatedCircleY; // Determine collision boolean collision = false; double distance = findDistance(unrotatedCircleX , unrotatedCircleY, closestX, closestY); if (distance < circle.radius) collision = true; // Collision else collision = false; |
1 2 3 4 5 6 7 8 9 10 11 12 13 | /** * Pythagorean theorem * @param fromX * @param fromY * @param toX * @param toY */ public double findDistance(double fromX, double fromY, double toX, double toY){ double a = Math.abs(fromX - toX); double b = Math.abs(fromY - toY); return Math.sqrt((a * a) + (b * b)); } |




circle.x and circle.y, are those the center points of the circle or the top-left corner?
Hi,
circle.x and circle.y on lines #2-5 are the center coordinates of the circle before being rotated.
I cant get it to work in my game.
Can you please have a quick check on my codes?
http://pastebin.com/FGpCtRNq
The comment on your code says your angles are in degrees. Those methods take angles in radians. Another thing it might be is the center of the graphic rotation. My sample’s graphic rotates with respect to the center of the rectangle.
Even though i don’t use Java, this tutorial was really helpful for me. The explanation helped me to solve an issue i was having while programming an collision system between circles and rectangles.
Thank you.
You could share your Collision Code ? I have this problem too.
I removed some words java and it worked perfectly in javascript. Thank you from Brazil.
Hi and thanks for a great bit of code.
I’ve ported this to Objective-C and changed the code to assume that it is the rectangles centre that is passed in. This allows it to be used more easily with the Cocos2D framework on iOS.
Here is a link: https://gist.github.com/pkclsoft/8293496
Awesome post – thank you!
I was able to translate your examples to a Javascript Canvas application with success. One thing I had to do differently was support negative and positive radians… I achieved that by converting any negative radians to their positive counterparts.
However, after making that adjustment I then needed to invert the radian value if the rectangle was in fact to be rotated with an originally positive value. Not sure if that makes any sense, it resulted in a few extra lines of code but it’s working great.
This article was really helpful for the Android Application I am making. BradGreens, thank you so much for leaving this comment because until I read it, I was struggling with an error as simple as flipping the radian values. I now flip the radian values (multiply by -1) if I start with positive degree values. Everyone else, make sure you do this if you are converting from degrees and think you are doing everything as according to this article but are still getting weird collisions.
It’s not working for me for some reason. It works for non-rotated rectangles. But when it comes to rotated rectangles it looks like it thinks they are rotating clockwise from its bottom left corner.
This helped me much since I am writing my first videogame with sdl 2.0 and following LazyFoo tutorial you linked.
Btw i’ ve got a little problem, the circle collide with the right angle, but after some testing I noticed that the higher is the angle the longer become the ‘invisible’ box, what am i doing wrong?
http://pastebin.com/raw.php?i=eEzEBu21
Hello, thank you for this code. If someone wants to use this on Andengine then angle variable must be like this: double angle=Math.toRadians(-sprite.getRotation());
Math.abs() in findDistance() is not necessary because a*a = |a|*|a| (e.g. (-2)*(-2)=4 and 2*2=4)
hey i just wanted to say thank you so much for the tutorial it really helped me a lot with my hittest for multiple moving rectangles. You are the best!!!!!!!!!!!!!!!!!!!!!
Hi!
I just want to thank you for this tutorial. It saved me a lot of trouble and finally gave me a good solution to collision detection. After a little tweak, it worked like a charm!
For all you JavaScript users there – the code itself didn’t work for me unless I’ve added a minus in front of every angle in Math.cos and Math.sin (it is same situation as fat2019 comment above), so it looked like that:
unrotatedCircleX = Math.cos( -rect.rotationInRadians) * ( circle.x – rectCenterX ) – Math.sin( -rect.rotationInRadians ) * ( circle.y – rectCenterY ) + rectCenterX;
unrotatedCircleY = Math.sin( -colidee.rotationInRadians ) * ( circle.x – rectCenterX ) + Math.cos( -rect.rotationInRadians ) * ( circle.y – rectCenterY ) + rectCenterY;
After this little operation collision detection works on every single angle I can think of!
Again, big thanks to you, Miguel Kano!
See: “2D Collision Detection for Game Programmers: Focus on Circle Collisions” on Amazon.com for a detailed answer to this question.
This question is not easily answered. There are 3 types of collision algorithms that may be written: Static, Semi-Dynamic, and Dynamic. Most of the discussions here were for Static collisions. Static collisions are when the algorithm assumes that the two objects are static, or not moving, even it they are actually moving. Semi-Dynamic collision algorithms account for object A moving, but assumes object B is static. Dynamic collision algorithms take into account that both objects are moving.
Static collision algorithms return only if a collision has occurred. The programmer only has the location of the objects to use for collision response. This is limiting, but sufficient for many games. Games like “Space Invaders” may be written using the algorithm. It is important to note that the static algorithms can have issues with small fast moving objects. Care must be taken to insure these objects cannot skip over each other in a single frame.
Semi-Dynamic collision algorithms return if a collision has occurred, The mathematical intersection point, the intersection time, the collision point (Where the two objects touch), and the collision normal. These algorithms take more time to execute, but return more information to allow for a wide variety of collision responses. This is the recommended algorithm I would use for most games. Games like “Break Out” may be written using this algorithm.
Dynamic collision algorithms return if a collision has occurred, the mathematical intersection point, the point where object A is at collision, the point where object B is at collision, the collision point, the collision normal for object A, and the collision normal for object B. This algorithm is the slowest to execute, but gives all the collision response details possible. This algorithm would be suitable to a “Break Out” like game that has multiple ball and if the balls collide they bounce off each other. Typically “Break Out” like game do not have the balls interacting with each other, therefore, the balls can occupy the same location with no response. This is not realistic, but how it is usually done.
The process for building the algorithms is fairly simple, but filled with a lot of repeating detail that make it cumbersome. The algorithms can be broken down into the following steps:
1) Identify the 2 objects to test for a collision
2) Create the collision area.
3) Test if the control point collides with any of the objects that make up the collision area. Divide and conquer decisions should be used to maximize efficiency.
The collision area is a composite of the 2 objects colliding. To create the collision object take object A and transcribe object A around object B. In the case of a circle colliding with an AABB, the collision area will have 4 circles at its corners, and 4 segments connecting the circles at their outer tangent points.
There is insufficient space in this blog give the algorithms in detail, but in the book “2D Collision Detection Algorithms for Game Programmers: Focus on Circle Collisions” will explain all 3 collision types for circles colliding with Points, Lines, Horizontal Lines, Vertical Lines, Rays, Segments, Circles, Ellipses, Axis Aligned Bounding Boxes (AABB), Object Oriented Bounding Boxes (OOBB), Capsules, and Polygons. I highly recommend this book.
You may also be interested in my other books also, they may be found at Amazon.com:
1) “2D Collision Detection for Game Programmers: Focus on Point Collisions”
2) “2D Collision Detection for Game Programmers: Focus on Circle Collisions”
3) “2D Collision Detection for Game Programmers: Focus on Ellipse Collisions”
In print soon:
4) “2D Collision Detection for Game Programmers: Focus on Axis Aligned Bounding Box (AABB) Collisions”
5) “2D Collision Detection for Game Programmers: Focus on Object Oriented Bounding Box (OOBB) Collisions”
6) “2D Collision Detection for Game Programmers: Focus on Capsule Collisions”
7) “2D Collision Detection for Game Programmers: Focus on Polygon Collisions”
8) “2D Collision Detection for Game Programmers: Focus on Collision Response”
Good luck with your game.