Sudoku Solver with recursive method
Sudoku Solver
Sudoku is a puzzle that uses numbers from 1 to 9 to match row, column, and 3×3 box with unique numbers.
I assume you are here because you want to learn how to find solutions to a Sudoku puzzle. I will show you how you can solve a Sudoku using recursive method. I will first explain what you have to do in English using pictures and then talk about codes in Java. This solution also works if you have cells preset as long as it’s valid.
You can download the demo program here and the whole project including source code here from github. For simplicity, the methods listed on bottom of this page are the ones used for “solving a Sudoku”.
Idea explained in plain English
1. Start from top left cell [0][0]. We will traverse from left-to-right and top-to-bottom.
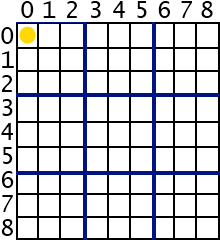
2. If this cell passed the end [8][8], we will be at [9][0] . If current row is 9, return true indicating it is done as we have gone through all of the cells. This is the first thing to check in the method.
3. Generate 9 randomly ordered unique numbers 1-9, so we can test them one by one.
![]()
4. Check if current number works, meaning no duplicates are found in its row, column, and 3×3 box.
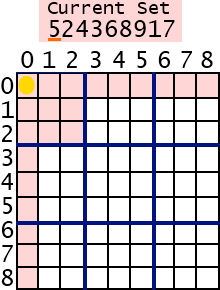
4a. If not duplicated, assign the current number to this cell.
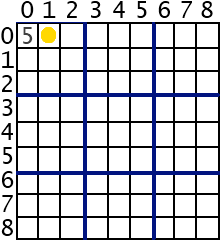
Move on to the next cell(call this method recursively). Repeat the steps from 2.
5. If this number is already contained, try the next number.
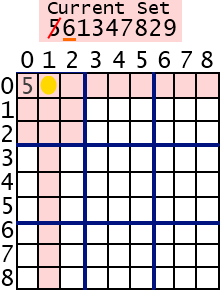
6. If none of the 9 numbers worked, return false indicating Sudoku is not complete, yet. This will return to the previous cell(Backtracking).
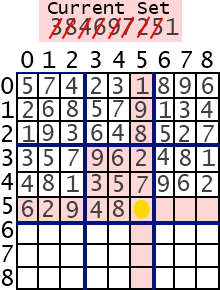
4b. Now, you have returned from the next cell. Set this cell blank because you assigned a number here once. Then continue from step 5 trying the next numbers.
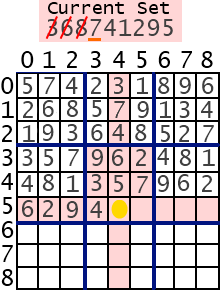
Implementation
First of all, I really recommend you make sure you are starting with a valid Sudoku. I will explain the essential part of the code by sections. You can see them entirely at the bottom of the page or play with the source code.
This is the step 2 from above. If we have gone through all of the cells, return true to start quitting from recursion.
1 2 | if (row == 9) return true; |
If this cell is not empty meaning it is preset, ignore and move on to the next cell.
1 2 3 4 | if (cells[row][col] != 0) { if (solve(col == 8? (row + 1): row, (col + 1) % 9)) return true; } |
In our else case when this cell is empty, we generate 9 unique numbers from 1 to 9 in random order. Then we set up a for-loop to iterate through 9 of them. We will test the numbers one at a time. If the number of current index is not found in its row, column, and 3×3 box, we assign this number to this cell and move on to the next cell.
We will return to this stage of method later on either when we finish the Sudoku or when the next cell could not find a number to place. The latter is called Backtracking. The method will continue from line 12 and have boolean value of false if we are backtracking. So it will fall into the else condition. We initialize this cell and keep going with the loop with next number. At the very end of this method which we reach if none of the 9 numbers worked, we return false to previous method.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | else { // Random numbers 1 - 9 Integer[] randoms = generateRandomNumbers(); for (int i = 0; i < 9; i++) { // If no duplicates in this row, column, 3x3, assign the value and go to the next if (!containedInRowCol(row, col, randoms[i]) && !containedIn3x3Box(row, col, randoms[i])) { cells[row][col] = randoms[i]; fields[row][col].setText(String.valueOf(randoms[i])); // Move to the next cell left-to-right and top-to-bottom if (solve(col == 8? (row + 1) : row, (col + 1) % 9)) return true; else { // Initialize the cell when backtracking (case when the value in the next cell was not valid) cells[row][col] = 0; fields[row][col].setText(""); } } } } return false; |
Sample Code
These methods are used to solve.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 | /** * Solve Sudoku recursively. * @param row current row index. * @param col current column index. * @return false if Sudoku was not solved. true if Sudoku is solved. */ private boolean solve(int row, int col) { // If it has passed through all cells, start quitting if (row == 9) return true; // If this cell is already set(fixed), skip to the next cell if (cells[row][col] != 0) { if (solve(col == 8? (row + 1): row, (col + 1) % 9)) return true; } else { // Random numbers 1 - 9 Integer[] randoms = generateRandomNumbers(); for (int i = 0; i < 9; i++) { // If no duplicates in this row, column, 3x3, assign the value and go to the next if (!containedInRowCol(row, col, randoms[i]) && !containedIn3x3Box(row, col, randoms[i])) { cells[row][col] = randoms[i]; fields[row][col].setText(String.valueOf(randoms[i])); // Move to the next cell left-to-right and top-to-bottom if (solve(col == 8? (row + 1) : row, (col + 1) % 9)) return true; else { // Initialize the cell when backtracking (case when the value in the next cell was not valid) cells[row][col] = 0; fields[row][col].setText(""); } } } } return false; } |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | /** * Check if a value contains in its 3x3 box for a cell. * @param row current row index. * @param col current column index. * @return true if this cell is incorrect or duplicated in its 3x3 box. */ private boolean containedIn3x3Box(int row, int col, int value) { // Find the top left of its 3x3 box to start validating from int startRow = row / 3 * 3; int startCol = col / 3 * 3; // Check within its 3x3 box except its cell for (int i = startRow; i < startRow + 3; i++) for (int j = startCol; j < startCol + 3; j++) { if (!(i == row && j == col)) { if (cells[i][j] == value){ return true; } } } return false; } |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | /** * Check if a value is contained within its row and column. * Used when solving the puzzle. * @param row current row index. * @param col current column index. * @param value value in this cell. * @return true if this value is duplicated in its row and column. */ private boolean containedInRowCol(int row, int col, int value) { for (int i = 0; i < 9; i++) { // Don't check the same cell if (i != col) if (cells[row][i] == value) return true; if (i != row) if (cells[i][col] == value) return true; } return false; } |
1 2 3 4 5 6 7 8 9 10 11 12 | /** * Generate 9 unique random numbers. * @return array containing 9 random unique numbers. */ private Integer[] generateRandomNumbers() { ArrayList<Integer> randoms = new ArrayList<Integer>(); for (int i = 0; i < 9; i++) randoms.add(i + 1); Collections.shuffle(randoms); return randoms.toArray(new Integer[9]); } |




Tank yo veru mócho.
:D:D
hi, thank you for all. that’s very good method for solving sudoku table. thanks alot brother